Simulating Tick Life Cycles Across Landscapes

yuval bloch

Model

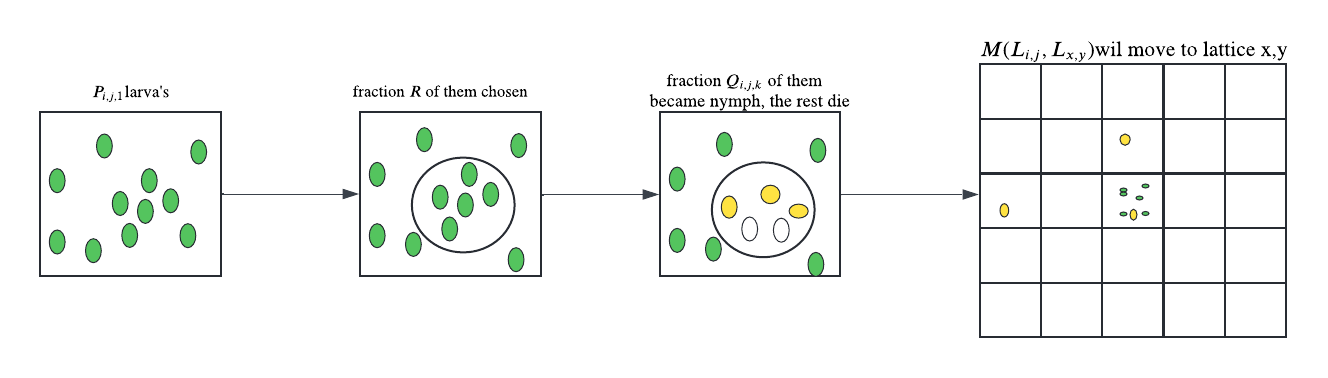
This model simulates tick population dynamics using a 3-layer lattice, where each layer corresponds to a life stage: larva, nymph, and adult. Ticks move both vertically between life stages and horizontally between geographic locations by biting a host.

Lattice and Tick Population

  • Each land cell is denoted by $L_{i,j}$, with a tick-carrying capacity $K_{i,j}$.

  • The population at life stage $s$ in cell $L_{i,j}$ is represented by $P_{i,j,s}$.

Tick model diagram
Figure 1. Each life stage is represented as a 2D lattice layer. Bites cause vertical (stage) and horizontal (spatial) movement.

Tick Movement and Life Cycle

To simplify, the model is first described in discrete steps:

At each time step:

  • A fraction $R$ of ticks in stage $s$ (i.e., $P_{i,j,s}$) attempt to transition.

  • A portion $Q(P_{i,j,s}, K_{i,j})$ of these successfully transition to stage $s+1$; the rest die.

  • New positions are selected via a movement kernel $M(L_{x,y}, L_{i,j})$, defining the probability of moving to each neighboring cell.

If the biting tick is an adult ($s = 3$), it reproduces by laying eggs, producing new larvae.

Tick model diagram
Figure 2.tick dynamic in one ”time step”, assuming only one cell populated with larva’s, and the rest are empty

Differential Equations

The change in tick population at each life stage is modeled using the following differential equations:

For nymphs and adults ($s > 1$):

$$ dPi,j,sdt=∑(x,y)∈N(i,j)R⋅Px,y,s−1⋅Q(Pi,j,s−1,Ki,j)⋅M(Lx,y,Li,j)−R⋅Pi,j,s\frac{dP_{i,j,s}}{dt} = \sum_{(x,y) \in N(i,j)} R \cdot P_{x,y,s-1} \cdot Q(P_{i,j,s-1}, K_{i,j}) \cdot M(L_{x,y}, L_{i,j}) - R \cdot P_{i,j,s} $$

For larvae ($s = 1$):

$$ dPi,j,1dt=∑(x,y)∈N(i,j)R⋅Px,y,3⋅Q(Pi,j,3,Ki,j)⋅M(Lx,y,Li,j)⋅E−R⋅Pi,j,1\frac{dP_{i,j,1}}{dt} = \sum_{(x,y) \in N(i,j)} R \cdot P_{x,y,3} \cdot Q(P_{i,j,3}, K_{i,j}) \cdot M(L_{x,y}, L_{i,j}) \cdot E - R \cdot P_{i,j,1} $$

Simulation Approach

The simulation uses a stochastic agent-based model based on the Gillespie algorithm, optimized via a decision tree (see Lester, 2020). Each agent represents a tick population at a specific stage and location.

Simulation Steps

  1. Select Agent: Each lattice cell is assigned an event rate of $P_{i,j,s} \cdot R$.

  2. Determine Event:

    • Bite: $\frac{Q_{i,j,k}}{1 + Q_{i,j,k}}$

    • Death: $\frac{1}{1 + Q_{i,j,k}}$

  3. If bite occurs:
    Select destination based on movement kernel $M(L_{x,y}, L_{i,j})$.

  4. If adult bites:
    Lay eggs following a normal distribution around $E$.

Infection Risk Estimation

Although the model does not explicitly include the Rickettsia pathogen, it assumes a $>$50% infection rate in the study area. Therefore, human bites are used as a proxy for infection risk, weighted by average tick density and human visitation per cell.